I. Методические рекомендации современному учителю.
Мы живем в быстро меняющемся мире, внедряются новые технологии, увеличивается объем знаний. Постепенно уходит в прошлое традиционная школа – школа объяснения знаний, всё активнее набирает силу школа нового исторического типа – школа развития. И современной школе нужен современный учитель.
А какой он – современный учитель?
1. Во-первых, это учитель, не просто в совершенстве знающий свой предмет, но и способный заинтересовать учеников и замотивировать их на его изучение. Одной из наиболее мощных мотиваций к изучению того или иного школьного предмета, безусловно, является понимание того, где приобретенные на уроках знания смогут пригодиться в реальной жизни. Начните изучение новой темы с яркого примера того, как данный материал может помочь в какой-либо конкретной ситуации.
В повседневной жизни любой человек, любой профессии практически ежедневно решает задачи это и физические и математические и логические задачи. Он рассчитывает свой бюджет, оплачивает счета, ходит в магазин, выбирает тариф интернета, телефонной сети, рассчитывает выгодные покупки, число калорий при диете, планирует, участвует в ремонте, строительстве, берет кредит и т.д., и т.п.
Практико-ориентированные задания по физике
2. Во-вторых, использующий в своей работе современные методы обучения, новейшее оборудование и цифровые технологии. Интерактивных инструментов в образовательном процессе становится все больше, они дают широкие возможности для привлечения внимания детей. Речь не только о стандартной компьютерной грамотности. Учитель должен понимать, какие цифровые инструменты окружают детей, по каким технологиям им удобнее и привычнее работать, тогда коммуникация между учителем и учениками будет эффективнее, а обучение быстрее принесет запланированный результат.
Использование цифровых лабораторий при изучении предметов естественно-научного цикла открывает новые возможности для решения учебных задач современной школы.
Федеральный государственный образовательный стандарт основного общего образования (ФГОС ООО) устанавливает требования к личностным, метапредметным и предметным результатам образования. И если предметные требования можно реализовать средствами отдельных учебных предметов, то требования к личностным и метапредметным результатам образования могут быть успешно реализованы лишь совместным и согласованным воздействием всех школьных предметов, курсов и модулей, входящих в основную образовательную программу школы. Одним из эффективных способов такого согласования является преподавание родственных учебных предметов на основе единой концепции, построенной на общих дидактических и технологических принципах.
Если в концентрированном виде формулировать основную цель естественнонаучного образования в основной школе, то ее можно определить как формирование естественнонаучной грамотности учащихся. Естественнонаучная грамотность – способность использовать естественно-научные знания, выявлять проблемы, делать обоснованные выводы, необходимые для понимания окружающего мира и тех изменений, которые вносит в него деятельность человека, и для принятия соответствующих решений. Это требует от естественнонаучно-грамотного человека следующих компетентностей: научно объяснять явления, оценивать и планировать научные исследования, научно интерпретировать данные и доказательства, использовать знания, полученные на уроках и во внеурочной деятельности для решения практических, жизненных задач. Естественнонаучная грамотность – это не только образовательная, но и гражданская характеристика, которая в большой мере отражает уровень культуры общества, включая его способность к поддержке научной и инновационной деятельности. Можно утверждать, что для осуществления технологической модернизации РФ естественнонаучная грамотность населения необходима в той же мере, в какой нужны и сами профессионалы – ученые, конструкторы, инженеры. Международное понимание естественнонаучной грамотности включает в себя ряд умений, или компетентностей, которые, в свою очередь, находятся в полном соответствии с требованиями ФГОС к образовательным результатам (см. таблицу 1).
Таблица 1
| Компетентности, определяющие естественнонаучную грамотность | Требования ФГОС ООО к результатам образования |
| понимание основных особенностей естественнонаучного исследования (или естественнонаучного метода познания) | приобретение опыта применения научных методов познания (предметный результат – физика); приобретение опыта использования различных методов изучения веществ (предметный результат – химия); приобретение опыта использования методов биологической науки (предметный результат – биология) |
| умение объяснять или описывать естественнонаучные явления на основе имеющихся научных знаний, а также умение прогнозировать изменения | умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач (метапредметный результат образования) |
| умение использовать научные доказательства и имеющиеся данные для получения выводов, их анализа и оценки достоверности | умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации, устанавливать причинно- следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы (метапредметный результат) |
Достаточный уровень овладения естественно-научной грамотностью означает приобретение учеником способности действовать, применяя освоенные предметные и метапредметные способы деятельности и умения (познавательные, информационные, коммуникативные, исследовательские и т.д.) для решения встречающихся в жизни проблем, связанных с естественными науками. Одним из средств формирования этих умений и способов деятельности является использование общих подходов к разработке учебных заданий в курсах химии, физики и биологии. Задания на материале каждого учебного предмета должны включать решение мировоззренческих, экологических и практико-ориентированных проблем в контексте реальных жизненных ситуаций.
Применение на уроках физики, химии, биологии цифровых лабораторий дает возможность формировать у учащихся метапредметные компетентности, определяющие естественнонаучную грамотность обучающихся.
Современный стандарт физического образования для средней школы требует активного освоения современных способов получения, обработки и представления информации, а также методов проведения исследовательских работ по физике. Поэтому задача внедрения компьютерной техники в подготовку, проведение экспериментальных работ и в обработку полученных экспериментальных данных является весьма актуальной.
Набор оборудования, сопровождающего его программного обеспечения «Цифровая лаборатория по физике» включает набор оборудования и датчиков. С помощью цифровой лаборатории можно:
– Провести работы базового уровня, позволяющие освоить идеологию и технику выполнения и обработки экспериментов с использованием цифровых датчиков, проводимых с пошаговой инструкцией и по жесткому сценарию;
– Расширить перечень и уровень сложности задач, так, чтобы они соответствовали изучению физики в 10-11 классах, в том числе на профильном уровне;
– Реализовать учебные исследования, используя методические рекомендации, в которых нет пошаговых инструкций, а имеется постановка задачи и рекомендации по ее решению, что способствует организации подготовке к ОГЭ и ЕГЭ по физике;
При переходе к работе с цифровой лабораторией по физике необходимо изучить интерфейс программы «Цифровая лаборатория», проведение видеосъемок физических явлений и его покадровой обработки.
Преимуществами использования цифровой лаборатории является следующее:
- Опыты проводятся с использованием реального физического оборудования, состыкованного с цифровыми датчиками, сигнал с которых поступает на компьютер и обрабатывается соответствующей программой, ученик для получения количественных данных должен осознать смысл сигнала. Компьютерная программа только ускоряет рутинные процедуры регистрации количественных данных: создание и заполнение таблиц, построение графика по табличным данным, подбор теоретической прямой (кривой), проходящей через все экспериментальные точки;
- Нет пошаговых инструкций к выполнению исследовательских работ. Ученик должен перейти к самостоятельному планированию эксперимента. Сам эксперимент в большинстве случаев предполагает проверку нескольких гипотез. Которая из них будет подтверждена в ходе эксперимента, ученик не знает (может не знать). После выполнения эксперимента обучающийся сам формулирует вывод.
- При обработке результатов не требуются жесткие сценарии. Ученику предоставляется удобный инструментарий по осуществлению сознательной выборки из всего массива полученных данных. В одном случае это все точки, зафиксированные датчиком, во втором – все данные из определенного интервала времени, в третьем – ряд отдельных точек, полученных в характерные моменты времени (например, когда физическая величина выходила на промежуточное, но стационарное значение). Ученик формирует внутри программы «Цифровая лаборатория» Таблицу данных для обработки, сохраняет ее в виде txt-файла, а затем переносит ее в редактор таблиц (например, MS Excel) и там ее обрабатывает.
Обработка может быть тоже весьма разнообразной – от построения графика по данным полученной таблицы до смещения отсчета времени, поточечного дифференцирования величин, пересчета данных с получением графика прямой, подбора функции, описывающей кривую и т.д. Этот подход заставляет ученика использовать знания, полученные на смежных предметах (информатики, математики).
Далее представлены исследовательские работы по физике с использованием цифровой лаборатории, которые формируют у учащихся исследовательские умения.
Исследовательская работа «Лабораторные исследования химического источника напряжения».
Цель работы: провести исследование получения источника напряжения химическим способом с применением цифровой лаборатории.
Оборудование: цифровая лаборатория, набор фруктов и овощей (лимон, яблоко, картофель, помидор), цинковый гвоздь, кусок медной проволоки.
Ход работы
- Запустите компьютер с установленной программой «Цифровая лаборатория». Загрузите программу «Цифровая лаборатория», подключите для снятия показаний датчик напряжения.
- Возьмите два электрода: 1- цинковый гвоздь, 2 – медная проволока, вставьте их в исследуемый фрукт или овощ. (см.рис.1)

- Подключите провода к электродам и поставьте в цепь датчик напряжения.
- Измерьте напряжение.
- Проведите эксперимент с имеющимися у вас фруктами и овощами.
Результаты измерений можно записать в таблицу 2
| Овощ/фрукт | Напряжение, В |
| Лимон | |
| Помидор | |
| Картофель | |
| Яблоко |
или представить в виде диаграммы рис.2 (пример)
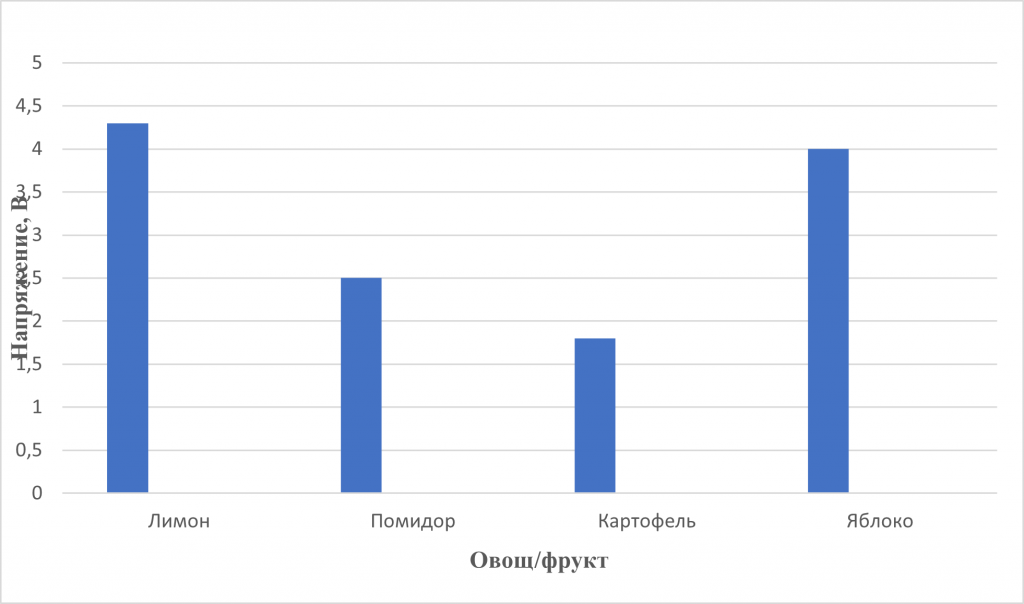
- Объясните полученные результаты. Насколько соответствуют экспериментальные данные ожидаемым?
Исследовательская работа «Лабораторные исследования зависимости давления от объема».
Цель работы: провести лабораторное исследование зависимости давления от объема с применением цифровой лаборатории.
Оборудование: цифровая лаборатория, набор «Датчик давления» и шприц.
Ход работы
- Ознакомьтесь с приборами для измерения давления:
Приборы для измерения давления
 |  |  |
| Барометр-анероид – прибор для измерения атмосферного давления | Манометр (металлический) – прибор для измерения давления в закрытых сосудах | Манометр (жидкостный) основан на измерении разности высот столбов однородной жидкости в сообщающихся сосудов. |
- Запустите компьютер с установленной программой «Цифровая лаборатория». Загрузите программу «Цифровая лаборатория», подключите для снятия показаний датчик давления.
- Возьмите шприц и выдвиньте до максимальной отметки по шкале.
- Замерьте давление датчиком, запишите значение давления и объема шприца в таблицу 4.
| V, мм3 | |||
| р, Па |
- Не вынимая датчика давления, сжимайте воздух до минимальной отметки по шкале и замерьте давление датчиком, запишите значение давления и объема шприца в таблицу 4
- Постройте график зависимости давления от объема.
- Объясните полученные результаты. Насколько соответствуют экспериментальные данные ожидаемым?
Использованием цифровых образовательных ресурсов при изучении школьных предметов служат и тесты-онлайн на различных платформах.
Проверочный тест по физике в Online Test Pad
Помочь ученику развиваться в этом сложном образовательном пространстве может только педагог, способный к мультидисциплинарному преподаванию на основе видения долгосрочной перспективы развития образования. Обладая сложным комплексом компетенций, в начальной школе он учитель. В основной, наставник проектных мастерских. А в старшей школе научный консультант. На протяжении всего образовательного процесса он воспитывает у детей представление об общечеловеческих ценностях, учит жить по принципам доброты и милосердия, терпимости и уважения. Помогает выстроить образовательный маршрут, учитывая сильные стороны ученика и опираясь на его интересы.
Презентация «Инструменты управления проектами или как упростить работу учителя»
3. В-третьих, современный учитель осознаёт значимость конвергентного подхода и междисциплинарной интеграции в школьном образовании. Он умеет разрабатывать конвергентные уроки, на которых используются межпредметные связи, что, в свою очередь, позволяет стирать границы между областями знаний, учит воспринимать мир как единое целое, а не как отдельные дисциплины, изучаемые в школе. Объясняя на своих уроках ту или иную тему, покажите учащимся, насколько ваш и другие школьные предметы взаимосвязаны между собой.
Связь физики с такими предметами как математика, химия, биология очевидна, есть общие темы, которые изучаются в математике и физике. Например, тема «Векторы», которая изучается в математике, широко применяется в физике при сложении векторных величин (силы, скорости, напряженности электростатического поля), без умения работать с буквенными выражениями (а эти умения формируются на уроках математики), невозможно упростить или преобразовать формулы по физике. В химии и физике есть общий раздел: Строения атома и атомного ядра, и знания по этой теме закладываются на уроках химии, а на уроках физике используются для определения строения ядра и составления ядерных реакций. В биологии процессы дыхания, и всасывания питательных веществ в кровь и ткани объясняется на основе, изученного физического понятия – диффузия.
Презентация «Конвергентное образование – шаг в будущее».
Но важно показать общее и между такими дисциплинами, где на первый взгляд, эта связь неочевидна. Например, физика и музыка или физика и изобразительное искусство. Музыка – это один из видов искусства, который передает авторское настроение, ценности, мысли и чувства с помощью звуков. Звук, в физике, это физическое явление, представляющее собой распространение упругих волн в газообразной, жидкой или твёрдой среде. Различные наборы звуков определяют тембр звука, различный набор звуков по-разному влияет на человека. Многие физики увлекались музыкой, виртуозно играли на музыкальных инструментах и сделав выбор в пользу науки, через всю жизнь пронесли любовь к музыке (Макс Планк, основоположник квантовой теории, был великолепным пианистом, Альберт Эйнштейн, создатель теории относительности, прекрасно играл на скрипке). И. Ньютон при разложении светового луча на световой спектр с помощью стеклянной призмы доказал зависимость цвета от длины волны. Ньютон определил, что в спектре семь цветов и сопоставил каждый цвет с музыкальным звуком (семь цветов в спектре, семь нот в музыке, ДО – фиолетовый, РЕ – синий, МИ – голубой, ФА – зеленый, СОЛЬ – желтый, ЛЯ – оранжевый, СИ – красный). Очень красивые явления игры цвета и света можно получить на цветомузыкальных установках. Таким образом, и звук и свет связаны одним физическим понятием волна, а волна характеризуется длиной волны, амплитудой, частотой и периодом колебаний.
Как можно использовать на уроках физики и математики умение играть в шахматы? Какие способности можно развить у обучающихся, если показать ребятам важность и ценность этих умений и заинтересовать их.
Презентация (математика+ физика) + шахматы
Умение играть в шахматы играет значительную роль при изучении математики и физики. Во-первых, игра в шахматы может развивать логическое мышление, аналитические навыки и стратегическое мышление, что является важным аспектом как в математике, так и в физике. В шахматах игроки должны думать несколько ходов вперед, распознавать шаблоны и соединять фланги, что также полезно для математического и физического мышления. Игра в шахматы также может помочь школьникам выработать навыки решения задач, принятия решений и анализа альтернатив.
В физике, шахматы могут помочь школьникам понять фундаментальные понятия, такие как векторы, стратегии движения и сложения сил. Они также могут использоваться для изучения теории игр и принятия оптимальных решений в различных ситуациях.
Таким образом, игра в шахматы может быть полезным инструментом при изучении математики и физики, помогая школьникам и студентам развивать свои умственные способности и понимание фундаментальных концепций.

Рихард Рети, чехословатский шахматист, гроссмейстер, писал «В юности у меня было два любимых занятия: математика и шахматы. Причина, по которой я предпочел шахматы математике может показаться непосвященному странной, а то и парадоксальной: в шахматах больше жизни, чем в математике». В тоже время математика является инструментом физики, а физика описывает мир математическими моделями и шахматы тоже являются моделью, которую можно использовать при изучении отдельных тем как физики, так и математики.
Формы мышления математика, физика и шахматиста довольно близки, и не случайно люди с математическим складом ума часто бывают способными шахматистами. Если рассматривать великих ученых, то и Карл Фредерик Гаусс и Леонард Эйлер всерьез увлекались шахматами и, физик П.Л. Капица, лауреат Нобелевской премии, серьезно увлекся шахматами в начале 20-х годов, когда был в научной командировке в Англии, где работал в лаборатории великого физика Э. Резерфорда. Петр Леонидович стал перед сном решать шахматные задачи и этюды, занятие настолько увлекло его, что он попытался сам составлять шахматные композиции. Итальянский ученый Галилео Галилей очень любил шахматы. Он в уме создавал шахматные комбинации и обдумывал стратегию партии. В шахматы Галилео играл до конца свой жизни — 77 лет. И только в 76 начал жаловаться на память — ему стало тяжело удерживать в уме партию целиком.
Шахматная доска сама по себе представляет достаточно интересный объект, посмотрим на легенду изобретения шахмат.

Шахматы появились в Индии более 1000 лет до н.э. Правитель был восхищён изобретением и пожелал наградить ученого, он пообещал выполнить любую просьбу мудреца и был удивлен его скромностью, когда тот пожелал получить в награду пшеничные зерна. На первое поле шахматной доски – одно зерно, на второе – два, на каждое последующее вдвое больше зёрен, чем на предыдущее. Царь приказал побыстрее выдать изобретателю шахмат его ничтожную награду.
Счетоводы магараджи работали всю ночь и только утром сообщили своему господину, что его повеление невыполнимо: такого количества зерна просто не было не только во всей Индии, но и на всей земле. Всего грозному владыке нужно было достать 18 квинтильонов 446 квадрильонов 744 триллиона 073 миллиарда 709 миллионов 551 тысячу 615 зерен. Для выполнения этой скромной просьбы мудреца потребовалось бы 280 000 лет подряд собирать весь выращенный урожай в Индии или же в течение 8 лет засеивать и собирать зерно со всей поверхности Земли. А если построить амбар дня него высотой четыре и шириной десять метров, то он был бы длиной в 300 000 000 километров, или от Земли до Солнца и обратно.
Как посчитать количество зерен на доске?
Количество зерен, находящихся на шахматной доске, не, что иное, как геометрическая прогрессия, первый член, которой равен 1, а знаменатель равен 2.
Sn = b1(qn-1)/ (q-1)

Шахматная доска представляет собой систему координат по горизонтальной оси наносятся латинские буквы (a, b, c, d, e, f, g, h) по вертикальной цифры (1-8). Система координат широко применяется в математике и физике, и познакомиться учащиеся с координатной плоскость могут гораздо раньше, чем в курсе математики и физики. Далее на слайдах представлены примеры использования координатной плоскости в математике, физике и шахматах. Если ребенок легко ориентируется на шахматной доске, может назвать координату фигуры и мысленно перемещая фигуру на шахматной доске изменять её координаты, то и при определении координат точки в декартовой системе координат, построении графиков у него не возникнет трудностей. А знакомясь в 7 классе с системой координат в физике он легко поймет, что оси координат могут обозначать и время, и скорость, и путь, а в 10 классе он легко будет строить графики и устанавливать зависимость термодинамических параметров.



Я хочу рассказать вам об одной из шахматных фигур – слон (или офицер), посмотрите на слайд и скажите, что объединяет эти темы математики и физики с шахматной фигурой слон.

В шахматах линии перемещения слона называют диагональю, а это и есть гипотенуза прямоугольного треугольника. В партии у вас есть два слона, и они отличаются друг от друга. Один может ходить только по полям белого цвета — такой слон называется белопольным. Другой слон ходит только по полям черного цвета и называется чернопольным. Слоны перемещаются по доске в любую сторону и на любое расстояние по полям одного цвета.
И ещё одно из общих понятий физики, математики и шахмат – это взвешивание.
Взвешивание (в физике, математике) – это определение массы тела, путем сравнения её с эталоном (за единицу массы в физике принят – 1 кг).
Определите вес (ценность) слона в единице шахмат – пешках, сравните его с другими шахматными фигурами.

Один из вариантов применения умения игры в шахматы при изучении физики — это использование аналогий между шахматами и физическими концепциями, чтобы облегчить понимание и запоминание материала. Например, вы можете представить различные части шахматной доски как различные элементы физической системы, или использовать правила шахматных ходов для объяснения физических законов. Игра в шахматы может быть полезной при изучении физики в школе, так как она развивает различные навыки: расчет и прогнозирование, концентрация и внимание, моделирование и умение выстраивать стратегию, эти умения и навыки в практической и профессиональной деятельности играют важную роль.
II. Методические рекомендации по подготовке рабочих программ в соответствии с федеральными основными общеобразовательными программами (ФООП).
Федеральная основная общеобразовательная программа (ФООП) – учебно-методическая документация (федеральный учебный план, федеральный календарный учебный график, федеральные рабочие программы учебных предметов, курсов, дисциплин (модулей), иных компонентов, федеральная рабочая программа воспитания, федеральный календарный план воспитательной работы), определяющая единые для Российской Федерации базовые объём и содержание образования определённого уровня и (или) определённой направленности, планируемые результаты освоения образовательной программы (п. 10.1. ФЗ-273). определённого уровня и (или) определённой направленности, планируемые результаты освоения образовательной программы (п. 10.1. ФЗ-273).



